字符串模式匹配AC自动机算法实现

孙康
  2024-08-24 10:12 2024-08-24 10:12 Created   2024-08-23 11:12:43 2024-08-23 11:12:43 Updated      1.4k Words  5 Mins  

AC 自动机（Aho-Corasick 算法）是一种线性时间复杂度的多模式字符串匹配算法。它能够在给定的文本中同时查找多个模式字符串，适用于需要快速查找的场景，如搜索引擎、文本编辑器和网络安全等。

AC 自动机的核心思想是利用 Trie 树（字典树）来存储模式字符串，并通过失配指针（Fail 指针）来优化匹配过程。失配指针基于 KMP 算法的思想进行构建，以避免重复查找。从而实现线性时间复杂度的匹配。

字典树构建

Trie 树是一种树形数据结构，用于存储字符串集合。每个节点代表一个字符，路径从根节点到某个节点表示一个字符串。Trie 树的优点是可以高效地进行前缀匹配。

这里以字符串集合{"mine", "my", "he", "she", "his", "hers"}为例，构成的字典树如下图：

字典树
字典树

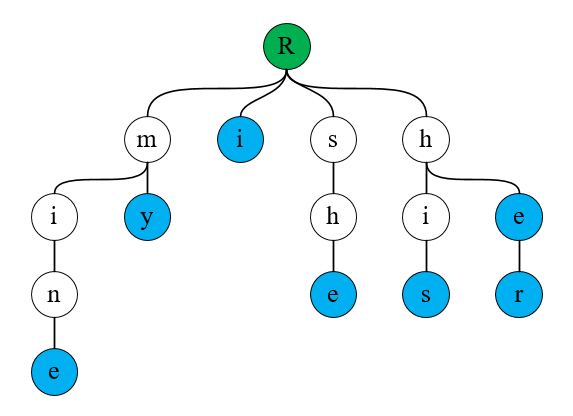
图中的根结点 R 是空结点，用于标识树的起点，其余结点代表一个字符，由根结点向下的任意一条路径表示一个字符串。在进行字符串插入时，从根结点开始遍历，逐个字符插入，如果当前字符的结点不存在则创建一个新结点。

为便于描述，对结点进行数据结构定义，这里将实际存储字符的数据描述为边，类型为映射，如果待存储的字符串仅包含英文字母，则这里可以简单将类型定义为长度为 26 的数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
type TrieNode struct {
	edges map[rune]*TrieNode
	isEnd bool
}

func NewTrieNode() *TrieNode {
	return &TrieNode{
		edges: make(map[rune]*TrieNode),
		isEnd: false,
	}
}

type TrieTree struct {
	root *TrieNode
}

字典树的构建过程很好理解，从根结点开始遍历，如果当前字符已有结点表示，则继续插入下一字符；如果当前字符没有表示结点，则创建新结点，并在当前字符串插入完毕后增加结束标记。

1
2
3
4
5
6
7
8
9
10
func (trie *TrieTree) Insert(pattern string) {
	node := trie.root
	for _, char := range pattern {
		if _, exists := node.edges[char]; !exists {
			node.edges[char] = NewTrieNode()
		}
		node = node.edges[char]
	}
	node.isEnd = true
}

失配指针构建

失配指针用于在匹配失败时，快速回退到可能的匹配位置。它指向当前节点的最长可匹配前缀的后缀节点。以上面构建的字典树为例，待匹配字符串为shers，匹配到字符e时，已经找到了匹配模式she，在继续向下匹配时，因为she分支已经没有向下的路径，所以需要切换分支，但我们不希望每次切换分支都从根结点开始重新匹配，毕竟当前已经知道待匹配字符串是包含she子串的，如果可以直接从前缀包含she后缀的分支开始匹配，则可以节省大量时间，而且最好选择的分支包含she后缀的深度最深。比如这里，我们希望切换分支匹配时直接切换到her分支的结点e上。

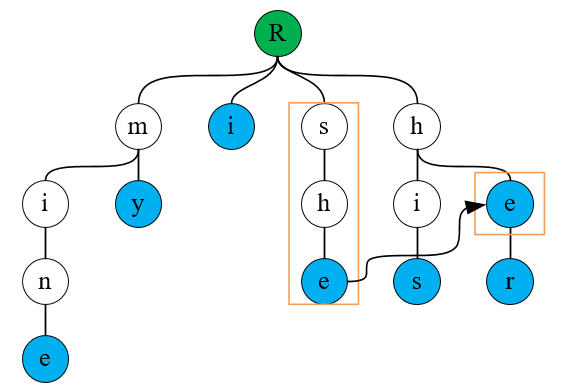
匹配失败切换分支
匹配失败切换分支

在构建失配指针时借用了 KMP 算法的思想，不了解该算法的不影响阅读本文，在构建失配指针时，遵循失配指针指向已匹配串的最长后缀分支，以上面的字典树为例，失配指针构建的结果如下：

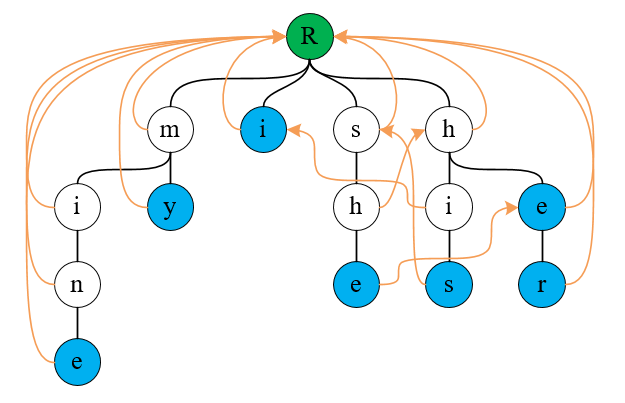
匹配失败切换分支
匹配失败切换分支

这里将上面字典树的数据结构稍作更改，实现失配指针的构建。构建失配指针使用广度优先搜索（BFS）来构建失配指针，即待构建层的上层结点均已完成失配指针的构建。对于字典树的每个结点，检查其子结点的失配指针，如果当前结点的失配指针指向的结点没有当前字符的子结点，则继续向上查找，直到找到一个有该字符的结点或到达根结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
type TrieNode struct {
	edges map[rune]*TrieNode
	isEnd bool
	fail  *TrieNode
}

type AhoCorasick struct {
	root     *TrieNode
	patterns map[*TrieNode]string
}

func (ac *AhoCorasick) BuildFailPointers() {
	queue := []*TrieNode{ac.root}

	for len(queue) > 0 {
		current := queue[0]
		queue = queue[1:]

		for char, edge := range current.edges {
			queue = append(queue, edge)

			fail := current.fail
			for fail != nil && fail.edges[char] == nil {
				fail = fail.fail
			}

			if fail != nil {
				edge.fail = fail.edges[char]
			} else {
				edge.fail = ac.root
			}
		}
	}
}

模式匹配

对给定字符串进行匹配时，从根节点开始，逐字符遍历文本。如果当前字符在当前结点的子结点中，则继续向下查找；如果不在，则通过失配指针回退。当到达一个结束结点时，表示找到一个匹配的模式字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func (ac *AhoCorasick) Search(text string) []string {
	node := ac.root
	results := make([]string, 0, len(text)/4)

	for _, char := range text {
		for node != nil && node.edges[char] == nil {
			node = node.fail
		}

		if node == nil {
			node = ac.root
			continue
		}

		node = node.edges[char]

		if node.isEnd {
			results = append(results, ac.patterns[node])
		}

		failNode := node.fail
		for failNode != nil {
			if failNode.isEnd {
				results = append(results, ac.patterns[failNode])
			}
			failNode = failNode.fail
		}
	}
	return results
}

总结

AC 自动机是一种高效的多模式字符串匹配算法，通过 Trie 树和失配指针的结合，能够在 O(n + m)的时间复杂度内完成匹配，其中 n 是文本长度，m 是模式字符串的总长度。

  • Title: 字符串模式匹配AC自动机算法实现
  • Author: 孙康
  • Created at : 2024-08-24 10:12:00
  • Updated at : 2024-08-23 11:12:43
  • Link: https://conradsun.github.io/2024/08db6e3319.html
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
字符串模式匹配AC自动机算法实现
  1. 字典树构建
  2. 失配指针构建
  3. 模式匹配
  4. 总结